最初にわり算の意味を指導を行います。等分除と包含除を並行対比して指導する方法と、わり算の計算が一段落するまで等分除のみの意味を指導する方法があります。
意味の指導を行った後は、九九の範囲の横書きの計算練習を行います。
素過程では、たて書きの計算に入りますが、《たてる》⇒《かける》⇒《ひく》⇒《おろす》の手続きのうち、ここでは《たてる》⇒《かける》⇒《ひく》までを行います。
除法の特徴
- 除法は加減乗除が順序よく複合されてできている
《たてる》
↓
《かける》【乗法】
↓
《ひく》【減法】
↓
《おろす》【加法】 - 除法は素過程に分解される
- 除法の計算法則は一貫しており、複合過程はその水源地に統一できる
素過程の指導
| 7÷3型 | |
|---|---|
|
7枚の切手があります。3人で分けると、1人で何枚もらえますか。 7 ÷ 3 = 2 あまり 1 |
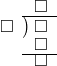 型 型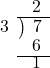 |
| 6÷3型 | |
| 余りのないタイプです。 |
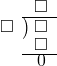 型 型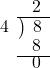 |
| 1÷3型 | |
|
2枚の切手を3人でわけようとおもいます。1人で何枚もらえるでしょう。 2 ÷ 3 = 0 あまり 2 商に0をたてられるかが鍵になります。 |
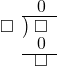 型 型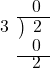 |
| 13÷3型 | |
|
13枚のハガキを4人でわけると、1人に何枚ずつあげればよいでしょう。 13 ÷ 4 = 3 あまり 1 商のたつ位置と、何を商にたてるかが鍵となります。 |
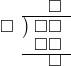 型 型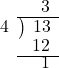 |
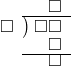
| 10÷3型 | |
|
この型は被除数から除数と商の積をひく減法が |
 型 型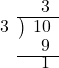 |