一般的な分数指導
最初にお断りしておくと、marimentでは、「一般的な分数指導」を行っています。
本稿でご紹介する共測量による分数指導は、現時点では指導研究課題であり、教材にもこの内容はありません。
しかし、分数の量の本質に迫る指導方法であり、機会があれば、夏休みのイベントなどで取り扱いたいと思います。
小数は、1未満のはしたを、十進位取り記数法により、![]() 、
、![]() 、
、![]() ・・・のスケールで測っていきます。
・・・のスケールで測っていきます。
いわば、分母が![]() (
(![]() は自然数)の単位分数
は自然数)の単位分数![]() ではしたを測る方法と言えます。
ではしたを測る方法と言えます。
子どもは、小数を分数で表す混合計算の学習単元で、この関係に気づくことができます。
これに対し、分数は、分母が![]() に固定されずに、自由に決めることができます。
に固定されずに、自由に決めることができます。
(「分母を自由に決める」「分母を求める」という表現に違和感を持つ方がいるのは当然です。我々もそうした学習体験はありませんし、教科書にも載っていません。もしかしたら、小数の学習でも、量を測る学習経験は十分とは言えなかったのではないでしょうか。こうした背景が本稿を記すきっかけとなりますので、馴染みにくいとは思いますが、最後まで読み進めて下さい。)
量を測る前に、小学校で分数はどのような場面で登場するでしょうか。
最初は、「いくつに分けたいくつ分」という分割分数と呼ばれる指導から始めるのが一般的です。ケーキを家族で分けるなど、分母は予め与えられています。この時、分ける対象が、![]() や、
や、![]() など普遍単位で表された場合を「分割量分数」と呼び、個別の量(ピザやケーキなど)を分ける分割分数と分ける場合があります。
など普遍単位で表された場合を「分割量分数」と呼び、個別の量(ピザやケーキなど)を分ける分割分数と分ける場合があります。
他に、割合分数、商分数(わり算を分数で表す)などに分類することができます。
前置きが長くなりましたが、このコラムでは、分母を予め与えられた数として認識するのではなく、分母を子供が導き出す指導方法について紹介します。
共測量を求めて分数で量を測る
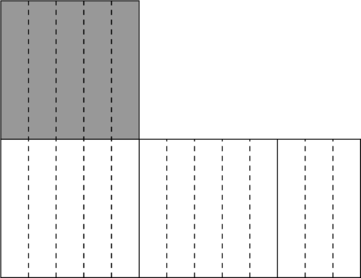
| Step1 |
|
|---|---|
|
測定対象の量(白いタイル)を基準となる量(グレーのタイル)で測ります。 2個分とはしたが出ます。 |
|
| Step2 |
|
|
基準となる量(グレーのタイル)を、Step1で求めた測定対象の量(白いタイル)のはした(=余り)で測ります。 1個分とはしたが出ます。 |
|
| Step3 |
|
|
Step2で求めた測定対象の量(白いタイル)のはしたを、Step2で求めた、基準となる量(グレーのタイル)のはした(=余り)で測ります。 1個分とはしたが出ます。 |
|
| Step4 |
|
|
Step3で求めた、基準となる量(グレーのタイル)のはしたを、Step3で求めた測定対象の量(白いタイル)のはしたで測ります。 2個分で割り切れました。 この例では、測定対象の量(白いタイル)のはしたが共測量となります。 |
|
| Step5 |
|
|
共測量を基準に、Step4からStep1に遡ると、共測量は基準量を5等分した量であることが求まり、分母が5と決定します。 今回の測定量は、 基準量を |
|